



Next: A.4 Modèles de croissance
Up: A. Compléments sur le
Previous: A.2 La règle d'or
Les résultats de ce modèle sont donc relativement frustrants.
A l'équilibre, la croissance est uniquement expliquée par des
facteurs exogènes.
Il est néanmoins possible d'obtenir plus d'information sur le
fonctionnement de cette économie en étudiant sa dynamique de
transition : la manière dont le revenu/tête converge sur sa valeur de
croissance équilibrée.
En divisant par 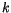 les deux membres de l'équation dynamique fondamentale,
nous obtenons
les deux membres de l'équation dynamique fondamentale,
nous obtenons
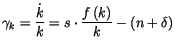 |
(A.13) |
où
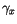 est le taux de croissance de la variable par tête
est le taux de croissance de la variable par tête 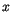 .
A chaque moment, le taux de croissance du niveau global de
.
A chaque moment, le taux de croissance du niveau global de 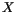 est donné
par
est donné
par
![\includegraphics[
height=8.0001cm,
width=9.999cm
]{solow6.eps}](img536.gif)
Convergence vers le SCE
Le sentier de croissance équilibrée est donc globalement stable :
![\includegraphics[
height=8.0001cm,
width=9.999cm
]{solow7.eps}](img537.gif)
Stabilité du SCE
Cette stabilité provient en fait des rendements déc
rois
sants du facteur capital.
Quand 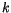 est relativement faible
est relativement faible
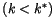 , la productivité moyenne du capital
, la productivité moyenne du capital
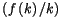 est relativement forte.
est relativement forte.
 les agents épargnent et investissent une part constante du revenu
et donc l'investissement brut par unité de capital,
les agents épargnent et investissent une part constante du revenu
et donc l'investissement brut par unité de capital,
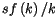 est fort;
est fort;
 la dépréciation du
la dépréciation du 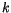 se fait à un taux constant
se fait à un taux constant
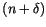 ;
;
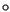 le taux de croissance
le taux de croissance 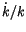 est donc positif et relativement fort.
(le raisonnement est inversé si
est donc positif et relativement fort.
(le raisonnement est inversé si
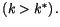 )
Dynamique du revenu/tête
Nous pouvons aussi calculer le taux de croissance du revenu/tête :
)
Dynamique du revenu/tête
Nous pouvons aussi calculer le taux de croissance du revenu/tête :
![$\displaystyle \gamma_{y}=\dot{y}/y=\frac{f^{\prime}\left( k\right) \dot{k}}{f\l...
...c{k\cdot f^{\prime}\left( k\right) }{f\left(
k\right) }\right] \cdot\gamma_{k}$](img544.gif) |
(A.14) |
L'expression
![$ \left[ \cdot\right] $](img545.gif) correspond à la part du
capital - la part de la rémunération du capital dans le revenu total
:
correspond à la part du
capital - la part de la rémunération du capital dans le revenu total
:
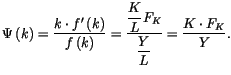 |
(A.15) |
Dans le cas d'une fonction Cobb-Douglas cette part est constante et elle est
égale à 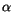 et donc le taux de variation du revenu/tête est
une fraction constante
et donc le taux de variation du revenu/tête est
une fraction constante 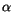 de
de
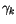 .
De manière générale, en utilisant l'équation A.13 :
.
De manière générale, en utilisant l'équation A.13 :
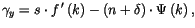 |
(A.16) |
Nous pouvons étudier comment ce taux de variation se modifie avec 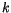 (sur
une trajectoire) :
(sur
une trajectoire) :
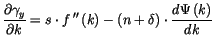 |
(A.17) |
![$\displaystyle \fbox{$\dfrac{\partial\gamma_y}{\partial k}=\underset{<0}{\underb...
...n+\delta\right) f\,^{\prime}}{f}\cdot\left[
1-\Psi\left( k\right) \right] }}$}$](img559.gif) |
(A.19) |
Nous avons deux cas :
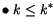
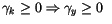 et et 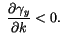 |
(A.20) |
Si le capital/tête croît, le revenu par tête croît aussi
mais de plus en plus faiblement.
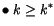
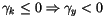 et et 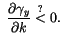 |
(A.21) |
Dans ce cas le premier terme devient positif et le résultat est ambigu.
Si l'on est proche de 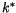 alors
alors
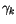 est très faible en valeur
absolue et le second terme négatif domine :
est très faible en valeur
absolue et le second terme négatif domine :
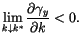 |
(A.22) |
Ce raisonnement est aussi valable pour la consommation/tête car
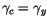 à chaque point du temps : la consommation
possède la même dynamique que le revenu.
à chaque point du temps : la consommation
possède la même dynamique que le revenu.




Next: A.4 Modèles de croissance
Up: A. Compléments sur le
Previous: A.2 La règle d'or
Yildizoglu Murat
2001-12-15
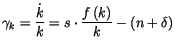
![\includegraphics[
height=8.0001cm,
width=9.999cm
]{solow6.eps}](img536.gif)
![\includegraphics[
height=8.0001cm,
width=9.999cm
]{solow7.eps}](img537.gif)
![$\displaystyle \gamma_{y}=\dot{y}/y=\frac{f^{\prime}\left( k\right) \dot{k}}{f\l...
...c{k\cdot f^{\prime}\left( k\right) }{f\left(
k\right) }\right] \cdot\gamma_{k}$](img544.gif)
![]() et donc le taux de variation du revenu/tête est
une fraction constante
et donc le taux de variation du revenu/tête est
une fraction constante ![]() de
de
![]() .
De manière générale, en utilisant l'équation A.13 :
.
De manière générale, en utilisant l'équation A.13 :
![$\displaystyle \fbox{$\dfrac{\partial\gamma_y}{\partial k}=\underset{<0}{\underb...
...n+\delta\right) f\,^{\prime}}{f}\cdot\left[
1-\Psi\left( k\right) \right] }}$}$](img559.gif)