Sous-sections

• 2.1.1 Axiomes pour les préférences

2.1 Le concept d'Utilité Espérée

L'incertitude existe quand le consommateur ne connaît pas parfaitement la situation dans laquelle il effectue son choix.

Exemple : Prendre ou non son parapluie en partant de chez soi le matin?

Si l'on connaissait parfaitement le temps qu'il va faire, ce serait un problème très simple :

$\longrightarrow$ Si pluie, prendre parapluie, sinon le laisser à la maison.

En général, on ne connaît pas avec certitude le temps qu'il fera.

Il existe une chance (plus ou moins forte selon la saison) qu'il fasse beau dans la journée.

Supposons qu'en ce mois, il pleuve dans 60% des cas.

Ainsi la conséquence de la décision ``prendre le parapluie'' dépend de la réalisation de l'événement ``Temps''.

Et comme on ne connaît pas avec certitude cette réalisation, la décision doit se faire en incertitude.

La réalisation de cet événement correspond à deux états de Nature possibles; un où il fait beau et un autre où il pleut.

---

Dans notre problématique, la réalisation de la condition aléatoire va correspondre à des situations différentes où le consommateur n'a pas les mêmes possibilités de consommation.

Appelons des lots ces différentes possibilités, comme s'il s'agissait en fait d'une loterie.

Soit $X$ l'ensemble de tous les lots possibles.

Définition 14   Une distribution de probabilité simple $p$ sur $X$ est spécifiée par

1. un sous-ensemble fini de $X$, appelé le support de $p$ et noté par $\sup p\left( p\right) ;$

2. pour tout $x\in\sup p\left( p\right) ,$ un nombre $p\left( x\right) >0,$ avec
   $$\sum_{x\in\sup p\left( p\right) }p\left( x\right) =1.$$

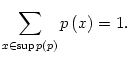
L'ensemble de toutes les distributions de probabilités simples sur $X$ est noté par $P$.

Les membres $p\in P$ seront donc appelés des loteries ou distribution de probabilités.

De même la loterie qui donne le lot $x$ avec la probabilité $1$ sera notée $\delta_{x}$.

Comment cette idée de loteries permet-elle de modéliser l'espace des biens en certitude?

S'il y a maintenant deux biens dans l'économie avec incertitude, on pourrait d'abord considérer un panier de biens comme étant un vecteur de loteries avec une distribution de probabilités $p_{1}$ pour les quantités du bien $1$ et $p_{2}$ pour le bien $2$: $\left( p_{1},p_{2}\right)$.

Mais ce n'est pas une bonne manière de procéder.

Nous allons plutôt considérer une distribution de probabilités sur les paniers de biens.

Pour pouvoir faire cela nous devons introduire un concept supplémentaire.

Soient $p$ et $q$ deux distributions simples de probabilités et $\alpha \in\lbrack0,1].$

Nous pouvons alors construire une nouvelle distribution de probabilités $r=\alpha p+\left( 1-\alpha\right) q$ en deux temps

$\left( i\right)$ Le support de la nouvelle distribution est l'union des supports de $p$ et de $q$: $\sup p\left( r\right) =\sup p\left( p\right) \cup\sup p\left( q\right) ;$

$\left( ii\right)$ Si $x$ est un membre de cette union $\left( x\in\sup p\left( r\right) \right)$, la probabilité associée à $x$ par la distribution $r$ est $r\left( x\right) =\alpha p\left( x\right) +\left( 1-\alpha\right) q\left( x\right)$ avec $p\left( x\right) =0$ si $x\notin\sup p\left( p\right)$ et, de manière similaire, $q\left( x\right) =0$ si $x\notin\sup p\left( q\right)$.

Exemple: Supposons que $p$ donne respectivement les probabilités $0.3,$ $0.1$ et $0.6$ pour les lots $x$, $y$ et $z$ et $q$ donne respectivement les probabilités $0.6$ and $0.4$ aux lots $x$ et $w.$

Soit $\alpha=1/3$.

Nous pouvons alors former $r=\left( 1/3\right) p+\left( 2/3\right) q$ de la manière suivante : le support de $r$ est $\{x,y,z,w\}$ et elle donne les probabilités suivantes pour ces lots:

• $r\left( x\right) =\left( 1/3\right) 0.3+\left( 2/3\right) 0.6=0.5$

• $r\left( y\right) =\left( 1/3\right) 0.1+\left( 2/3\right) 0=0.033$

• $r\left( z\right) =\left( 1/3\right) 0.6+\left( 2/3\right) 0=0.2$

• $r\left( w\right) =\left( 1/3\right) 0+\left( 2/3\right) 0.4=0.266$

On appelle parfois $r=\left( 1/3\right) p+\left( 2/3\right) q$ une loterie composée dont les lots sont $p$ et $q$.

2.1.1 Axiomes pour les préférences

Supposons maintenant que les préférences du consommateurs $\left( \succ\right)$ sont définies sur l'ensemble $P$ des distributions simples de probabilités sur $X$.

Hypothèse 3   $\succ$ doit être asymétrique et négativement transitive.

Hypothèse 4   Axiome de substitution. Soient $p$ et $q$ deux distributions de probabilités telles que $p\succ q$. Soit $\alpha \in\left( 0,1\right)$ et $r$ une autre distribution de probabilités. Alors, $\alpha p+\left( 1-\alpha\right) r\succ\alpha q+\left( 1-\alpha\right) r$.

Hypothèse 5   Axiome d'Archimède. Soient $p,q$ et $r$ des distributions de probabilités telles que $p\succ q\succ r$. Alors les nombres $\alpha,\beta\in\left( 0,1\right)$ tels que

$$\alpha p+\left( 1-\alpha\right) r\succ q\succ\beta p+\left( 1-\beta\right) r$$

existent.

Proposition 10   Fonction d'utilité espérée. Une relation de préférence $\succ$ sur l'ensemble $P$ des distributions simples de probabilités sur l'espace $X$ vérifient les Hypothèses  $\left( \ref{vnma1}- \ref{vnma3}\right)$ si et seulement s'il existe une fonction $u:X\rightarrow\mathbb{R}$ telle que

$$p\succ q\Leftrightarrow\sum_{x\in\sup p\left( p\right) }u\left( x... ...x\right) >\sum_{x\in\sup p\left( q\right) }u\left( x\right) q\left( x\right) .$$

De plus, si $u$ nous donne une représentation de ce type de $\succ$ alors $v$ le fait tout aussi bien s'il existe des constantes $a>0$ et $b$ telles que $v\left( \cdot\right) \equiv au\left( \cdot\right) +b$.

Remarque 8   Cette proposition établit l'existence d'une représentation numérique des préférences sur $p$: il existe une fonction $U:P\rightarrow\mathbb{R}$ telle que $p\succ q$ si et seulement si $U\left( p\right) >U\left( q\right) .$

Remarque 9   Elle établit aussi le fait que cette fonction $U$ doit prendre la forme d'une espérance mathématique d'utilité

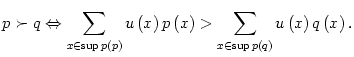
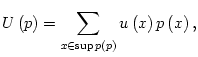$$U\left( p\right) =\sum_{x\in\sup p\left( p\right) }u\left( x\right) p\left( x\right) ,$$ pour une fonction $$u:X\rightarrow\mathbb{R}$$.

Problème 10   Supposons qu'il y ait deux situations possibles avec deux niveaux de revenu différents:deux états de la Nature, $d$ et $f.$ Soit $\pi,$ la probabilité de réalisation de l'état $d$ et $1-\pi$, celle de $f.$ A ces états correspondent respectivement les revenus $R_{d}$ et $R_{f}$.

1. Représentez cette loterie sous forme d'arbre. Calculez l'espérance des gains.

2. Donnez la fonction d'utilité espérée $U$ de l'agent.

3. Donnez la définition du $TMS_{f,d}$ en partant du différentiel total de l'utilité espérée. Quelle est la signification de ce TMS?

4. Chaque loterie de ce type s'écrit $\left( \pi,R_{d},R_{f}\right)$. Comparez les loteries $p=\left( 0.5,25,75\right)$ et $q=\left( 0.25,100,25\right)$ si la fonction d'utilité de l'agent est $u\left( .\right) =Ln\left( .\right)$ pour déterminez son choix.

5. Les loteries se caractérisent en termes de biens $\left( \pi ,x_{d},x_{f}\right)$ et la fonction d'utilité du consommateur est $u\left( x_{1},x_{2}\right) =x_{1}x_{2}$. Donnez la fonction d'utilité espérée $U$. Donnez le $TMS_{f,d}^{1}$ pour le bien $1$. Comparez les loteries $\left( 0.25,\left( 10,90\right) ,\left( 20,20\right) \right)$ et $\left( 0.4,\left( 20,30\right) ,\left( 30,40\right) \right) .$