



Next: D.2 Consommation optimale
Up: D. Modèle de Ramsey.
Previous: D. Modèle de Ramsey.
Ramsey a cherché à déterminer l'épargne qu'une nation doit
effectuer dans une perspective dynamique.
La population, 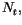 croît au taux
croît au taux 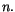 On peut la voir comme une
famille unique ou comme des familles identiques se développant dans le temps.
Chaque adulte offre une unité de main d'oeuvre et donc, l'offre de travail
est égale à la population.
La production est réalisée à partir de cette main d'oeuvre et du
capital,
On peut la voir comme une
famille unique ou comme des familles identiques se développant dans le temps.
Chaque adulte offre une unité de main d'oeuvre et donc, l'offre de travail
est égale à la population.
La production est réalisée à partir de cette main d'oeuvre et du
capital, 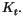 Il n'y a pas de progrès technique.
Le produit est soit consommé, soit investi :
Il n'y a pas de progrès technique.
Le produit est soit consommé, soit investi :
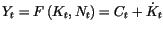 |
(D.1) |
Nous exclurons la dépréciation du capital. La fonction
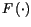 est néo-classique.
En termes per capita, cette équation devient :
est néo-classique.
En termes per capita, cette équation devient :
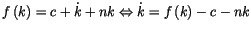 |
(D.2) |
L'économie démarre avec un capital/tête 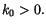 Au moment
Au moment 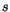 l'utilité instantanée de la famille est donnée, en
valeurs courantes, par :
l'utilité instantanée de la famille est donnée, en
valeurs courantes, par :
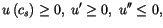 |
(D.3) |
on l'appelle aussi la fonction de ``félicité" (ou de ``bonheur").
A ce moment 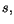 l'utilité d'une consommation qui a lieu à un moment
l'utilité d'une consommation qui a lieu à un moment
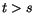 est donnée en valeurs actualisées par :
où
est donnée en valeurs actualisées par :
où 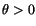 est la préférence pour le présent ou le taux
d'escompte subjectif.
Si l'on considère l'utilité totale jusqu'à la fin des temps
(l'infini), on peut l'écrire, en temps continu et en valeurs
actualisées au moment
est la préférence pour le présent ou le taux
d'escompte subjectif.
Si l'on considère l'utilité totale jusqu'à la fin des temps
(l'infini), on peut l'écrire, en temps continu et en valeurs
actualisées au moment 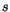 :
:
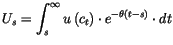 |
(D.4) |




Next: D.2 Consommation optimale
Up: D. Modèle de Ramsey.
Previous: D. Modèle de Ramsey.
Yildizoglu Murat
2001-12-15