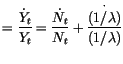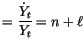Next: B.3 Le second problème
Up: B. Le modèle keynésien
Previous: B.1 Équilibre du marché
Cela correspond à la condition
A l'équilibre, la constance de la technologie et des prix doivent conduire
à un coefficient marginal du facteur-travail constant
 |
(B.10) |
La condition d'équilibre
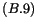 devient alors
qui nous donne le niveau de production qui permet d'employer toute la
population active. Cette condition peut aussi être exprimée en termes
de taux de croissance (dérivée loga
rithmique)
devient alors
qui nous donne le niveau de production qui permet d'employer toute la
population active. Cette condition peut aussi être exprimée en termes
de taux de croissance (dérivée loga
rithmique)
En dérivant les deux membres de cette égalité, on obtient les
dérivées logarithmiques donc, des taux de croissance
où 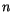 est le taux de croissance de la population et
est le taux de croissance de la population et 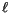 est le taux de
croissance de la productivité du travail.
est le taux de
croissance de la productivité du travail. 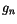 est le taux de
croissance naturel qui rend compatible l'évolution de la
production et celle de la population active de manière à ne pas
créer du chômage.
Par conséquent, nous devons avoir l'évolution suivante
est le taux de
croissance naturel qui rend compatible l'évolution de la
production et celle de la population active de manière à ne pas
créer du chômage.
Par conséquent, nous devons avoir l'évolution suivante




Next: B.3 Le second problème
Up: B. Le modèle keynésien
Previous: B.1 Équilibre du marché
Yildizoglu Murat
2001-12-15