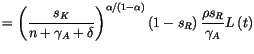Remarque 3
Un cas particulier élimine ce résultat et cela correspond à la
fonction de production des idées du modèle originel de Romer
(1990):
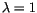
et
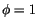
et donc la croissance est possible même avec un effort constant de
recherche car la productivité de recherche
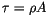
est croissant
dans le temps même si le nombre de chercheurs est constant. Même s'il
est séduisant, cette idée de Romer est en contradiction avec les faits
car les taux de croissance des économies occidentales n'ont pas
considérablement augmenté pendant le siècle dernier malgré une
croissance très forte de l'effort de recherche et de développement. Ce
résultat empirique implique
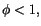
comme nous l'avons supposé.
Remarque 4
Dans tous les cas de figure, des politiques économiques ne peuvent
influencer le taux de croissance d'une telle économie car aucune des
variables figurant dans l'équation
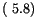
n'est
influencée par les politiques habituelles malgré le fait que le
progrès technique soit maintenant endogène.
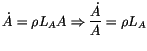
![\includegraphics[
trim=0.000000in 0.000000in -0.004042in 0.000985in,
height=6.0231cm,
width=8.2461cm
]{GR51.eps}](img297.gif)
![\includegraphics[
height=6.0231cm,
width=11.5147cm
]{GR52.eps}](img308.gif)